Boids are, per Wikipedia,

an artificial life program, developed by Craig Reynolds in 1986, which simulates the flocking behaviour of birds, and related group motion.

This blog covers a naive implementation of a Boids algorithm in Julia.

Basic Idea.

We have some pre-defined number of objects — boids — in an arena of size $(L, W)$. These objects have some properties associated with them. Notably, position in the arena (maybe something like boid.posx, boid.posy) and velocity, (maybe something like boid.velx, boid.vely).

We can create a mutable struct in Julia to represent each boid:

mutable struct Boid{T <: Number} # To start
	vel::Vector{T}
	pos::Vector{T}
end

function Boid(vel::Vector{T}, pos::Vector{T}) where T <: Number
	return Boid{T}(vel, pos)
end

As well as a struct for the arena:

struct Arena{T <: Number}
	h::T
	w::T
end

Each boid updates it's position by taking at step in the direction of it's velocity vector:

function boid_position_update!(current_boid::Boid{T}, arena; δt = 0.1) where {T <: Number}
	
	current_boid.pos[1] = current_boid.pos[1] + δt * current_boid.vel[1])
	
	current_boid.pos[2] = current_boid.pos[2] + δt * current_boid.vel[2])
	return nothing
end

If we initialize at some random distribution of initial position and velocities, the boids will slowly wander out of the arena:

boids = [Boid(
    [rand(Normal(0, 7)), rand(Normal(0, 7))], 
    [rand(Uniform(0, test_arena.w)), rand(Uniform(0, test_arena.h))]
) for _ in 1:200]

So instead of updating to:

We'll mod out the size of the arena, for example:

This makes it more like a game of pac-man –- if we lose a boid along the edge of the screen, they'll pop back up, having wrapped around the opposite side.

Boid Behaviour.

Most boid implementations seem to use the following rules:

1. Boids have two nested detection ranges –- a "vision range", and an "avoidance range".

2. Inside the vision range, boids will steer towards other boids.

3. Inside the avoidance range, boids will steer away from other boids.

4. Inside the vision range, boids will try to match their velocity to those of the boids around them

Optionally, there are some other rules, e.g.

1. Boids will steer to avoid walls.

2. Boids belong to different groups, and will only flock with "friends"

3. Boids will fly towards a target, or away from a predator.

and many more. This initial implementation focuses on mostly the first rules, with the addition of wall avoidance.

Implementation of Rules One, Two, Three

Each boid struct is modified to include a parameter for detection range and avoidance range.

mutable struct Boid{T <: Number}
    vel::Vector{T}
    pos::Vector{T}
    
    detection_range::T
    avoidance_range::T
end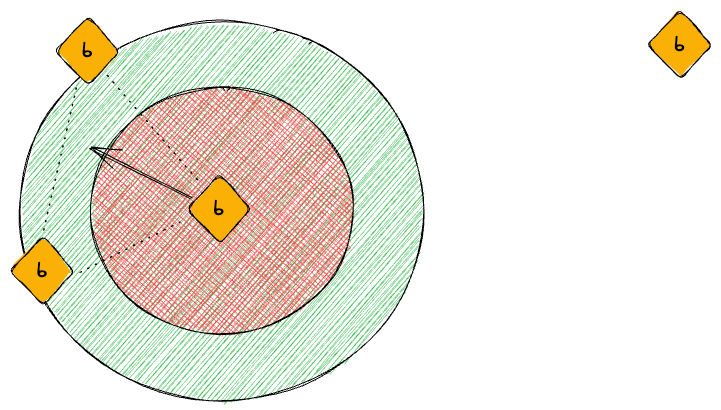

(WIP: Up to this point, just a trial to make sure my mp4 compression is working well with github pages)